A Few Years Ago the News Magazine the Economist Listed

question 65

Essay

A few years ago the news magazine The Economist listed some of the stranger explanations used in the past to predict presidential election outcomes.These included whether or not the hemlines of women's skirts went up or down,stock market performances,baseball World Series wins by an American League team,etc.Thinking about this problem more seriously,you decide to analyze whether or not the presidential candidate for a certain party did better if his party controlled the house.Accordingly you collect data for the last 34 presidential elections.You think of this data as comprising a population which you want to describe,rather than a sample from which you want to infer behavior of a larger population.You generate the accompanying table:
Joint Distribution of Presidential Party Affiliation and Party Control
of House of Representatives,1860-1996
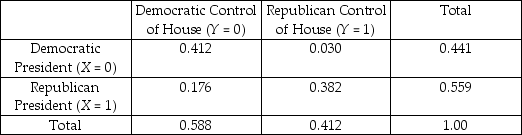(a)Interpret one of the joint probabilities and one of the marginal probabilities.
(b)Compute E(X).How does this differ from E(X 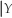= 0)? Explain.
(c)If you picked one of the Republican presidents at random,what is the probability that during his term the Democrats had control of the House?
(d)What would the joint distribution look like under independence? Check your results by calculating the two conditional distributions and compare these to the marginal distribution.

---

Definitions:

Issuing Company

A corporation that has put into circulations its shares or bonds to raise capital by selling those securities to investors.

Legal Liabilities

Obligations arising from laws or regulations that a company is required to pay, such as fines, settlements, or judgments.

Sick Pay Payable

A liability account that represents the amount of sick pay owed to employees but has not yet been paid.

Notes Payable

Liabilities representing amounts borrowed by a company that must be repaid, often with interest, as evidenced by a promissory note.