The Gallup Poll Frequently Surveys the Electorate to Quantify the Public's

question 23

Essay

The Gallup Poll frequently surveys the electorate to quantify the public's opinion of the president.Since 1945,Gallup settled on the following wording of its presidential poll: "Do you approve or disapprove of the way (name)is handling his job as president?" Gallup has not changed its presidential question since then,and respondents can answer "approve," "disapprove," or "no opinion."
You want to see how this approval rating is related to the Michigan index of consumer sentiment (ICS).The monthly survey,conducted with a minimum sample of 500,asks people if they feel "better/worse off" with regard to current and future conditions.
(a)To estimate dynamic causal effects,you collect quarterly data from 1962:I - 1998:II for the United States.You allow a binary variable for each presidency to capture the intrinsic popularity of the President.Furthermore,you eliminate observations that include a change in party for the presidency by using a binary variable,which takes on the value of one during the first quarter of the year after the election.Finally,a friendly political scientist provides you with (i)an "events" variable, (ii)a "Vietnam" binary variable,and (iii)a "honeymoon" variable,which measures the effect of a higher popularity of a president immediately following the election.(The coefficients of these variables will not be reported here. )
Assuming that consumer sentiment is exogenous,you estimate the following two specifications (numbers in parenthesis are heteroskedasticity- and autocorrelation-consistent standard errors): t = 26.08 + 0.178 × ICSt + 0.232 × ICSt-1;R2= 0.667,SER = 7.00
(8.83)(0.120)(0.135) t = 26.08 + 0.178 × ΔICSt + 0.411 + ICSt-1;R2 = 0.667,SER = 7.00
(8.17)(0.120 )(0.089)
What is the difference between the two specifications? What is the advantage of estimating the second equation,if any?
(b)Assuming that the errors follow an AR(1)process,you also estimate the following alternative: 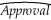t = -4.61 + 0.300 × ICSt - 0.070 × ICSt-1- 0.054 × ICSt-2;+ 0.776 × Approvalt-1;
(5.84)(0.083)(0.099)(0.083)(0.057)
R2 = 0.868,SER = 4.45
How is this specification related to the previous ones? What implicit assumptions did you have to make to allow for desirable properties of the OLS estimator?
(c)You finally estimate the approval equation using the quasi-difference specification and the GLS estimator. How is this equation related to the ones in (a)and (b)? What are the properties of the GLS estimator here,under the assumption that ICS is strictly exogenous?
(d)Is it likely that the ICS is exogenous here? Strictly exogenous?

Recognize effective strategies for enhancing students' self-esteem and participation in the classroom.

Evaluate the quality and variability of Head Start programs and their impact on early childhood education.

Understand strategies for improving interethnic relations and fostering inclusive learning environments.

Understand the definition, symptoms, and characteristics of ADHD.

---

Definitions:

Standard Deviation

A measure of the amount of variation or dispersion of a set of values, showing how much the values differ from the mean.

Mean

The average of a set of numerical values, calculated as the sum of the values divided by the number of values.

Mean

The arithmetic average of a set of numbers, calculated by adding them together and dividing by the number of quantities.

Point Estimate

A single value estimate of a population parameter that serves as the best guess or prediction of the parameter.