Solved

TABLE 13-12
the Manager of the Purchasing Department of a Large

question 77

Multiple Choice

TABLE 13-12
The manager of the purchasing department of a large banking organization would like to develop a model to predict the amount of time (measured in hours) it takes to process invoices. Data are collected from a sample of 30 days, and the number of invoices processed and completion time in hours is recorded. Below is the regression output:
$\begin{array}{l}\text { Regression Statistics }\\\begin{array} { l c } \hline \text { Multiple R } & 0.9947 \\\text { R Square } & 0.8924 \\\text { Adjusted R Square } & 0.8886 \\\text { Standard Error } & 0.3342 \\\text { ations } & 30 \\\hline\end{array}\end{array}$

$\begin{array}{lrrccc}\hline & \text { d f } & \text { SS } & \text {MS} & \text { F } & \text { Significance F } \\\hline \text {Regression} & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm{E}-15 \\ \text {Residual }& 28 & 3.1282 & 0.1117 & & \\ \text {Total }& 29 & 29.072 & & & \\\hline\end{array}$

$\begin{array}{lrrrrrr}\hline & \text { Coefficients }& \text { Standard Error }& \text { t Stat }& \text { p -value}& \text {Lower 95\%} & \text {Upper 95\%} \\\hline \text { Invoices }& 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \text {Processed }& 0.0126 & 0.0008 & 15.2388 & 4.3946 \mathrm{E}-15 & 0.0109 & 0.0143 \\\hline\end{array}$

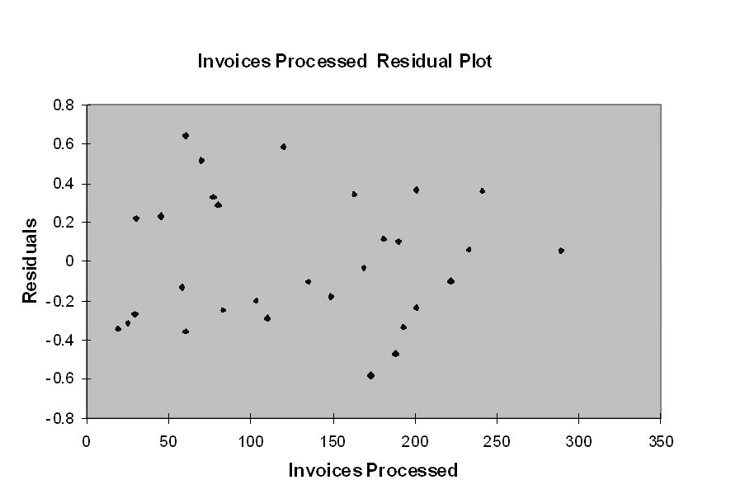
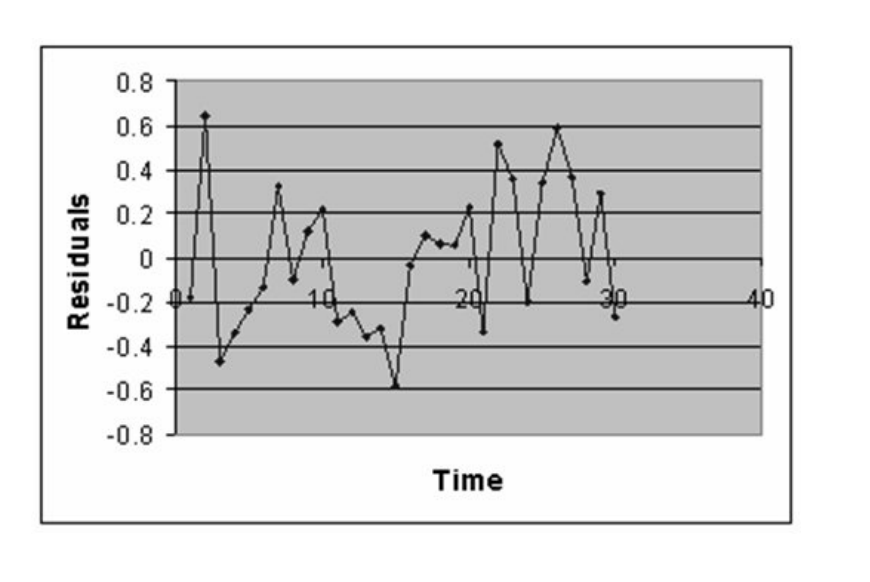
$TABLE 13-12 The manager of the purchasing department of a large banking organization would like to develop a model to predict the amount of time (measured in hours) it takes to process invoices. Data are collected from a sample of 30 days, and the number of invoices processed and completion time in hours is recorded. Below is the regression output: \begin{array}{l} \text { Regression Statistics }\\ \begin{array} { l c } \hline \text { Multiple R } & 0.9947 \\ \text { R Square } & 0.8924 \\ \text { Adjusted R Square } & 0.8886 \\ \text { Standard Error } & 0.3342 \\ \text { ations } & 30 \\ \hline \end{array} \end{array} \begin{array}{lrrccc} \hline & \text { d f } & \text { SS } & \text {MS} & \text { F } & \text { Significance F } \\ \hline \text {Regression} & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm{E}-15 \\ \text {Residual }& 28 & 3.1282 & 0.1117 & & \\ \text {Total }& 29 & 29.072 & & & \\ \hline \end{array} \begin{array}{lrrrrrr} \hline & \text { Coefficients }& \text { Standard Error }& \text { t Stat }& \text { p -value}& \text {Lower 95\%} & \text {Upper 95\%} \\ \hline \text { Invoices }& 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \text {Processed }& 0.0126 & 0.0008 & 15.2388 & 4.3946 \mathrm{E}-15 & 0.0109 & 0.0143 \\ \hline \end{array} -Referring to Table 13-12, the error sum of squares (SSE) of the above regression is A) 0.1117. B) 29.0720. C) 25.9438. D) 3.1282.$

$TABLE 13-12 The manager of the purchasing department of a large banking organization would like to develop a model to predict the amount of time (measured in hours) it takes to process invoices. Data are collected from a sample of 30 days, and the number of invoices processed and completion time in hours is recorded. Below is the regression output: \begin{array}{l} \text { Regression Statistics }\\ \begin{array} { l c } \hline \text { Multiple R } & 0.9947 \\ \text { R Square } & 0.8924 \\ \text { Adjusted R Square } & 0.8886 \\ \text { Standard Error } & 0.3342 \\ \text { ations } & 30 \\ \hline \end{array} \end{array} \begin{array}{lrrccc} \hline & \text { d f } & \text { SS } & \text {MS} & \text { F } & \text { Significance F } \\ \hline \text {Regression} & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm{E}-15 \\ \text {Residual }& 28 & 3.1282 & 0.1117 & & \\ \text {Total }& 29 & 29.072 & & & \\ \hline \end{array} \begin{array}{lrrrrrr} \hline & \text { Coefficients }& \text { Standard Error }& \text { t Stat }& \text { p -value}& \text {Lower 95\%} & \text {Upper 95\%} \\ \hline \text { Invoices }& 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \text {Processed }& 0.0126 & 0.0008 & 15.2388 & 4.3946 \mathrm{E}-15 & 0.0109 & 0.0143 \\ \hline \end{array} -Referring to Table 13-12, the error sum of squares (SSE) of the above regression is A) 0.1117. B) 29.0720. C) 25.9438. D) 3.1282.$

-Referring to Table 13-12, the error sum of squares (SSE) of the above regression is

Definitions:

Milgram Experiment

A psychological experiment conducted by Stanley Milgram in the 1960s to study obedience to authority, where participants were instructed to administer electric shocks to another person.

Stanford University Prison Experiment

A psychological study conducted by Philip Zimbardo in 1971 at Stanford University, where students were assigned roles of prisoners and guards to explore the effects of perceived power.

Generalization

Drawing a conclusion about a certain characteristic of a population based on a sample from it.

Logical Support

The provision of reasons or evidence to justify a claim or argument.

TABLE 13-12 the Manager of the Purchasing Department of a Large

Definitions:

TABLE 13-12
the Manager of the Purchasing Department of a Large