Assume that two presidential candidates,call them Bush and Gore,receive 50% of the votes in the population.You can model this situation as a Bernoulli trial,where Y is a random variable with success probability Pr(Y = 1)= p,and where Y = 1 if a person votes for Bush and Y = 0 otherwise.Furthermore,let 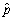 be the fraction of successes (1s)in a sample,which is distributed N(p,
be the fraction of successes (1s)in a sample,which is distributed N(p, 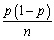 )in reasonably large samples,say for n ≥ 40.
)in reasonably large samples,say for n ≥ 40.
(a)Given your knowledge about the population,find the probability that in a random sample of 40,Bush would receive a share of 40% or less.
(b)How would this situation change with a random sample of 100?
(c)Given your answers in (a)and (b),would you be comfortable to predict what the voting intentions for the entire population are if you did not know p but had polled 10,000 individuals at random and calculated 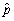 ? Explain.
? Explain.
(d)This result seems to hold whether you poll 10,000 people at random in the Netherlands or the United States,where the former has a population of less than 20 million people,while the United States is 15 times as populous.Why does the population size not come into play?
Definitions:
Monthly Interest Rate
The interest rate charged or earned, expressed on a monthly basis, typically used for loans or investments.
Monthly Interest Rate
It's the interest rate applied each month on loans, savings, or investments, calculated by dividing the annual interest rate by 12.
Q5: Uncertainty of future sales and cost of
Q8: Think of at least nine examples,three of
Q9: The interpretation of the slope coefficient in
Q18: Given the relationship between the two variables,the
Q35: (Requires Appendix material)Your textbook states that in
Q38: What role does the concept of cointegration
Q41: You have collected quarterly data on inflation
Q44: The reason why estimators have a sampling
Q47: You should use the QLR test for
Q57: In nonlinear models,the expected change in the